Parallèle entre grossissement et focale.
- 21 janvier 2017
Comment évaluer le grossissement à partir de la focale et inversement.
Ou comment faire le parallèle entre grossissement et focale équivalente en photographie d’une lunette d’observation.
Dans cet article, nous allons essayer de répondre à une question qui m’a bien souvent été posée. « Dites-moi, votre super téléobjectif, il grossit combien de fois ? » ou encore « Quelle focale atteignez-vous avec votre longue vue ? ». Commençons par expliquer les mentions que l’on retrouve habituellement sur les jumelles et les lunettes d’approche que nous utilisons à des fins d’observation ornithologique ou autre d’ailleurs. Nous essayerons ensuite d’évaluer le rapport entre grossissement et focale d’une paire de jumelle, d’une longue vue ou d’un objectif photographique. Nous verrons enfin quels renseignements utiles nous pouvons en tirer afin de choisir et d’utiliser au mieux ces différents outils.
Tout d’abord, soyons clair, des jumelles ou une longue vue ne possèdent pas de focale propre, pas plus que de diaphragme contrairement à un objectif photo. De même, un objectif photo n’est jamais caractérisé par un grossissement mais bien par une focale et une ouverture maximum de son diaphragme (par exemple « Canon EF 300mm 1:2.8 L IS USM » ou 300 mm représente la focale et 1:2.8 l’ouverture maximale de son diaphragme).
Le grossissement.
Le grossissement est défini comme étant le rapport de la dimension angulaire de l’image à la dimension angulaire de l’objet. Donc le grossissement
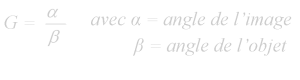
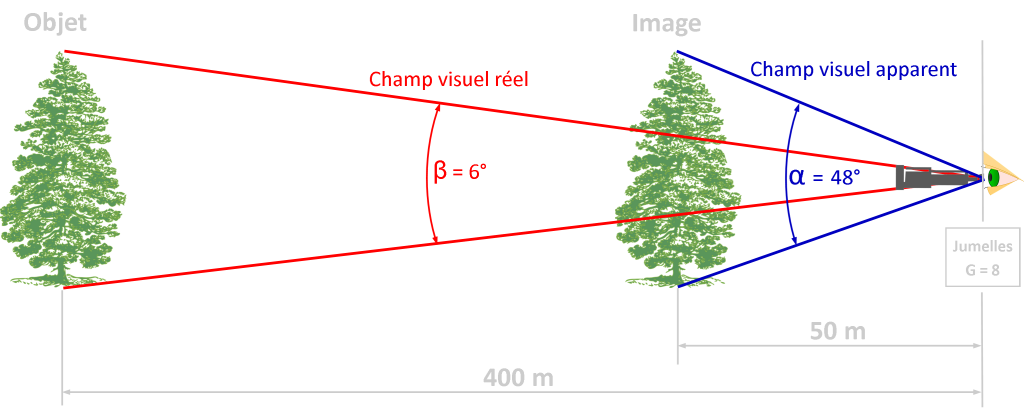
D’après le schéma ci-dessus, on peut aussi admettre qu’un objet paraîtra être 8 fois plus proche de l’observateur en utilisant des jumelles de G = 8. Ceci est une définition plus communément admise et surtout comprise par la plupart des personnes.
Voyons maintenant si nous pouvons faire un rapprochement entre la focale d’un objectif et son grossissement équivalent. Cela sera plus facile à appréhender par tout un chacun alors qu’une longueur focale ne représente souvent qu’une donnée abstraite.
Il est admis que l’œil humain possède un grossissement de 1. Nous savons aussi qu’il est communément accepté qu’un objectif ayant une longueur focale de 50 mm fournisse une vision très proche de la vision de notre œil, il a donc aussi un grossissement de 1. En fait et pour les puristes, cette focale est de 43 mm. Nous nous contenterons de la très bonne approximation de 50 mm pour la suite de notre propos. Partant de là, on peut dire que le grossissement d’un objectif photo est égal à sa longueur focale divisée par 50.
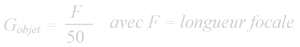
Dès lors, un super téléobjectif qui affiche 500mm 1:4 fournit un grossissement de 10x (500/50=10) et sa luminosité est représentée par le chiffre 4 (aussi indiqué par f/4). Ce chiffre ne possède pas de dimension. Il représente en fait le diamètre maximum utilisable de l’ouverture du diaphragme, donc la quantité maximum de lumière qui atteindra la pellicule ou le capteur numérique. Ce diamètre peut être calculé à l’aide de la formule suivante
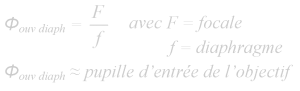
Pour notre téléobjectif à pleine ouverture le diaphragme a un diamètre de 125 mm (f/4) et de 15,6 mm à sa plus petite ouverture (f/32). Notons que la pupille d’entrée à ouverture maximum du diaphragme est aussi le diamètre de la lentille frontale de l’optique. On voit que, à focale constante, si le nombre de diaphragme augmente, le diamètre d’ouverture de celui-ci diminue. Donc, plus le nombre de diaphragme que vous sélectionnez sur votre appareil est grand, plus le « trou » par lequel passera la lumière pour atteindre le capteur numérique sera petit. Ceci se traduit par une perte de lumière qui sera compensée par une vitesse d’obturation plus lente ou une augmentation de la sensibilité du capteur (les fameux ISO).
Les jumelles
Quelles sont les renseignements que l’on retrouve en général sur une paire de jumelles ?
Première indication :
10 x 42
Le premier nombre représente le grossissement des jumelles et le deuxième donne le diamètre de la lentille frontale. De ce qui précède, nous pouvons dire que la focale équivalente de ces jumelles est de
F = G x 50 = 10 x 50 = 500 mm
N’oublions toutefois pas que des jumelles ne possèdent pas de longueur focale et que cette conclusion est purement indicative à des fins d’éventuelle comparaison avec un objectif photographique.
Le deuxième nombre nous donne le diamètre de la lentille frontale. Ceci est une très bonne indication de la luminosité des jumelles. En effet, plus cette lentille est grande, plus la quantité de lumière qu’elle absorbera ou laissera passer est grande. Donc, à grand nombre, grande luminosité.
Deuxième indication :
FOV 341 FT ou 346 FT @ 1000 YDS / 115 M @ 1000 M
Le champ visuel réel (Field Of View FOV) Il s’agit du champ angulaire observé à partir du centre des objectifs des jumelles. Il est donné par le constructeur en degrés (par exemple 6,6°). Les fabricants l’expriment le plus souvent en un nombre de mètres à 1000 mètres ou un nombre de pieds (feet) à 1000 yards, ce qui plus facile à appréhender pour le commun des mortels. Plus le grossissement est faible, plus le champ visuel réel est large, et inversement, un grossissement plus fort donne un champ visuel plus étroit. Par conséquent, les champs visuels réels de jumelles à grossissement différent ne sont pas comparables.
Il faut admettre que 346 pieds à 1000 yards ne me dit pas grand-chose. Nous ne sommes pas habitués aux pieds et encore moins aux yards. Il est toutefois facile de calculer que 1 pied @ 1000 yards vaut 0,333 m @ 1000 m et 1 m @ 1000 m est égal à 3,003 pieds @ 1000 yards. Donc 346 pieds @ 1000 yards = (346 x 0,333) m @ 1000 m = 115,2 m @ 1000 m.
Le champ visuel exprimé en degrés est beaucoup moins souvent mentionné sur les jumelles elles-mêmes. Il faudra consulter la documentation technique pour le trouver. Il faut bien admettre que, à nouveau, cette expression du champ visuel en degrés est plus difficile à se représenter. Petite digression trigonométrique. On sait qu’un milliradian est un angle qui intercepte un arc de 1 mm à 1 mètre, 1 mètre à 1000 mètre (tiens donc…) etc…
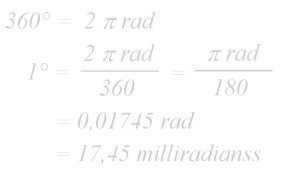
Il en découle qu’un degré soutien un arc de 17,45 mètres à une distance de 1000 mètres. Aussi, le champ visuel de 115 mètres à 1000 mètres équivaut à 115/17,45 = 6,59 degrés. De même, 6,59 degrés représentent un champ visuel de 17,45 x 6,59 = 115 mètres à 1000 mètres.
La pupille de sortie

Aussi appelé cercle oculaire, c’est le point lumineux rond que l’on observe lorsque l’on tient les jumelles à bout de bras et qui représente le diamètre en millimètres de l’image de la lentille frontale donnée par l’oculaire. Il est défini par le rapport du diamètre de la lentille frontale divisé par le grossissement. Par exemple pour une paire de jumelles 10×42 : 42/10 = 4,2 mm.
Idéalement ce diamètre doit être égal à celui de la pupille de l’œil pour une utilisation optimale de la lumière. Si la pupille de l’œil est différente de la pupille de sortie, on constate une perte plus ou moins importante de luminosité. Dans l’obscurité, les pupilles se dilatent afin de permettre de mieux voir. Inversement, dans la lumière du jour, elles se contractent afin de limiter la quantité de lumière atteignant la rétine pour éviter l’éblouissement. Cette dilatation ou contraction des pupilles devient de plus en plus difficile avec l’âge, la pupille étant moins souple. Le diamètre de notre pupille se situe en plein jour entre 2 et 3 mm, au crépuscule entre 4 et 6 mm et la nuit aux alentours de 7 mm.
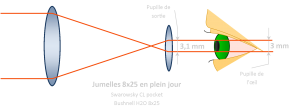
La pupille de l’œil humain s’ouvrant de 2 à 3 mm maximum en plein jour. Les pupilles de sortie des jumelles devraient mesurer 3 mm environ.
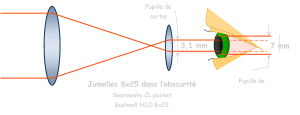
La nuit par contre, nos pupilles se dilatent jusqu’à 7 mm dans l’obscurité, une pupille de sortie d’environ 3 mm ne transmettra pas suffisamment de lumière, ce qui rendra l’image sombre.
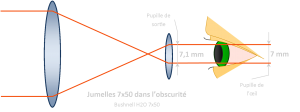
Les jumelles destinées à un usage nocturne doivent donc être dotées de larges pupilles de sortie ce qui les rend malheureusement plus lourdes et donc nettement plus encombrantes.
Indice crépusculaire
Ce chiffre indique la qualité optique d’une jumelle par mauvaise luminosité. Il s’obtient en extrayant la racine carrée du produit du diamètre de la lentille frontale et du grossissement. Par exemple pour une paire de jumelles 10×42 :√(10×42) = √420 = 20,49. Les jumelles qui conviennent le mieux à l’observation nocturne sont celles dont l’indice crépusculaire égale ou dépasse 49. Il faut cependant relativiser ce résultat car il tend à favoriser les gros diamètres. De plus il est pratiquement impossible à atteindre avec des jumelles. Il faudrait considérer une optique de 20×120 per exemple !!!
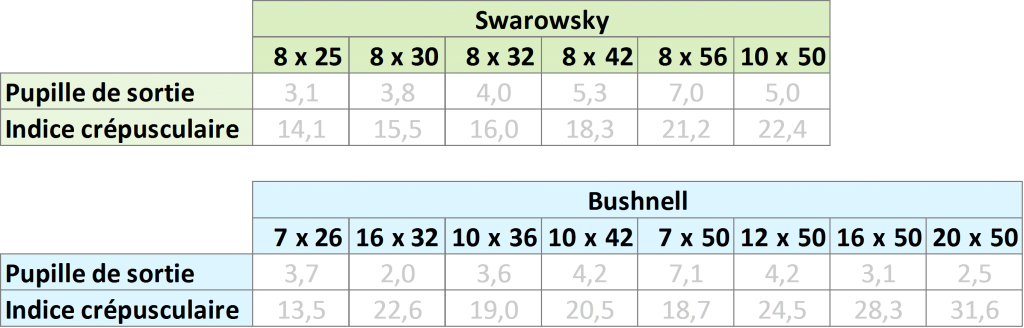
Le tableau suivant donne les pupilles de sortie et les indices crépusculaires des jumelles les plus communes de deux marques connues.
La longue vue
Tout ce qui a été dit précédemment concernant les jumelles reste valable et d’application pour une longue vue. Reprenons la fiche de données techniques de la Swarowsky ATS/STS 80 HD.
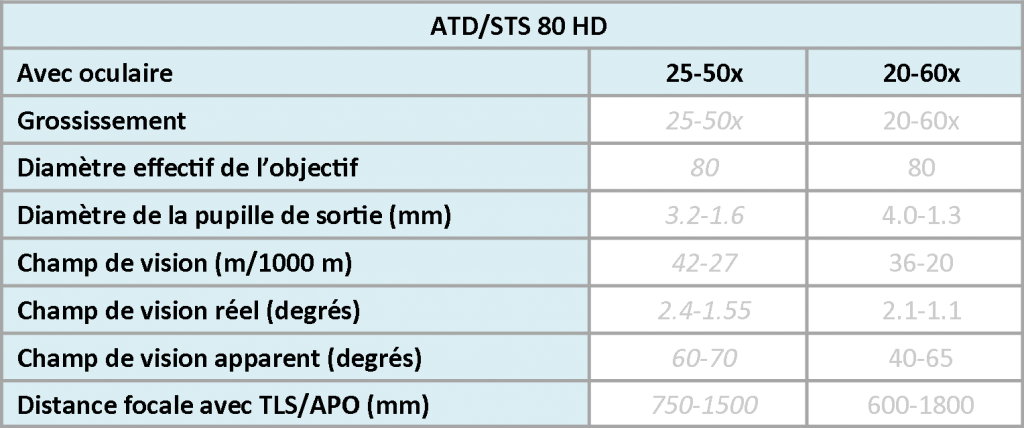
Prenons comme exemple la lunette équipée d’un oculaire 25-50x.
1. Grossissement.
Il correspond au premier nombre caractérisant les jumelles (10x42). Nous avons ici deux nombres car il s’agit d’un zoom grossissant de 25x à 50x.
2. Diamètre effectif de l’objectif.
Il s’agit du diamètre de la lentille frontale tout comme pour les jumelles. Il correspond au deuxième nombre (10x42). On peut considérer qu’il représente aussi la dimension de la pupille d’entrée de la longue vue.
3. Diamètre de la pupille de sortie.
Nous utilisons la même formule pour calculer sa valeur. Pupille de sortie = Ø/G = 80/25 = 3,2 et 80/50 = 1,6
4. Champ de vision et champ de vison réel.
Donnés et probablement mesurés par le fabricant, nous pouvons les vérifier à l’aide de la conversion suivante : 1° = 17,45 mètres à 1000 mètres.
2,4 ° correspond à 2.4 x 17.45 = 41.88 m @ 1000 m
1,55 ° correspond à 1.55 x 17.45 = 27.04 m @ 100 m
5. Champ de vision apparent.
Il représente l’angle sous lequel l’image est vue au travers de l’oculaire.
Il peut se calculer par G x champ de vision réel. Donc 2.4° x 25 = 60°
6. Le problème de la focale.
Comme mentionné plus haut, la focale est égale au grossissement x 50 (G x 50). Dès lors il est raisonnable de considérer une focale équivalente pour cette longue vue variant entre 1250 mm et 2500 mm. Pour la digiscopie, il faudra adjoindre à cette lunette un appareil photo, reflex par exemple, équipé de son propre objectif. Cet objectif possède naturellement son propre grossissement calculé par la formule G = focale / grossissement. Dans le cas du TLS/APO, sa focale étant de 30 mm, son grossissement est de 0,6. Celui de l’ensemble lunette/TLS/APO varie donc entre 0,6 x 25 = 15 et 0,6 x 50 = 30. Nous pouvons maintenant recalculer la focale de l’ensemble et nous trouvons 750 mm à 25x et 1500 mm à 50x.
